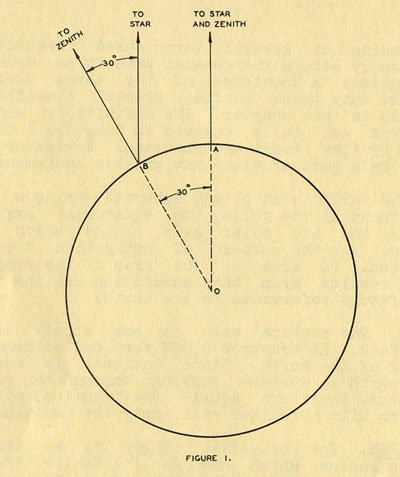FIGURE I.

Let an observer on the earth be at the geographical position of a heavenly body, as at A, in Figure 1. At this position the particular body and the observer's zenith are apparently one. Since the celestial bodies (with one exception for the present) may be assumed to be at an infinite distance from an observer on the earth, the particular body being considered will be seen in the same direction in space when the observer has moved to position B, 1800 nautical miles from A, measured along a great circle on the earth. At position A the altitude of the body obviously is 90 degrees and its zenith distance 0. At position B, though the body appears in the same direction in space, its altitude and zenith have changed, this being occasioned by the shift in the positions of the observer's zenith and horizon resulting from his change of position.

From the definition of 'nautical mile, the Great Circle are joining A and B subtends an angle of 1800 minutes, or 30 degrees at the earth's center. The change in the position of the observer's zenith after moving from A to B obviously is 30 degrees since the radii OA and OB, bounding the 30 degree angle at the earth's center, when prolonged, intersect the celestial sphere at the zenith of the two positions.

A study of Figure 1 shows that when the observer is at position B the body's zenith distance is 1800 minutes of angle (or 30 degrees); this equalling, exactly, the number of nautical miles the observer is removed from the point vertically beneath that celestial body, that is, from its geographical position.

An observer situated at the geographical position of a particular heavenly body could move 1800 miles away from that position along any one of an infinite number of great circles radiating from that position. Consequently, there must be an infinite number of points on the earth from which the body's zenith distance would measure 30 degrees (and its altitude, 60 degrees) at the same instant. Test would soon indicate that all these points lay in a small circle of exactly 1800 nautical miles radius, having the geographical position as its center; and apart from such tests it is apparent that, if the earth be a sphere, this must be the case. Such a circle is known as a position circle; an observer being at all times situated on one of the position circles of every heavenly body visible from his position.

Altitude and zenith distance are two terms used very frequently in celestial navigation. It is vitally necessary that their meanings be clearly committed to memory. Also, they must be associated so completely that the mention of one term automatically calls the other to mind. It is the altitude of a heavenly body that is always measured, and not its zenith distance. Yet it will be seen from later subject matter and illustrations that it is the zenith distance which is a part of the astronomical triangle that is solved in each problem. It must be automatically realized that when the celestial triangle is solved for the computed zenith distance, the corresponding computed altitude is available, or that when the altitude is found by measurement with the sextant the corresponding "measured" zenith distance is available.

Though no visible star exactly marks the position of the north celestial pole (Polaris is roughly one degree removed), let it be assumed for the present that one does. An observer who finds the altitude of the star now marking the exact position of the celestial pole to be 90 degrees would know himself to be situated at its geographical position, the north terrestrial pole. The observer's latitude clearly is 90 degrees and the zenith distance of the celestial pole 0 degrees, thus:

Latitude Zenith Distance Altitude
90. . . . .0. . . . . . . . . . . .90

Now let the observer move 600 miles (nautical) away from the pole along a great circle. Substituting the terrestrial pole for A in Figure 1 and redrawing the figure so that the observer's new position is 600 miles or 10 degrees from the pole, it becomes apparent that the following figures are correct for the coordinates under which they are written:

Latitude Zenith Distance Altitude
80. . . . .10. . . . . . . . . . .80

If the observer moves to the earth's equator in 600 miles, or 10 degree increments, the following tabulated values are obviously correct for the three coordinates:

Latitude Zenith Distance Altitude
90. . . . .0. . . . . . . . . . . .90
80. . . . .10. . . . . . . . . . .80
70. . . . .20. . . . . . . . . . .70
60. . . . .30. . . . . . . . . . .60
50. . . . .40. . . . . . . . . . .50
40. . . . .50. . . . . . . . . . .40
30. . . . .60. . . . . . . . . . .30
20. . . . .70. . . . . . . . . . .20
10. . . . .80. . . . . . . . . . .10
0. . . . . .90. . . . . . . . . . .0

If the reader is at all dubious as to the correctness of the above tabulated figures, he should convince himself of their correctness by drawing several figures similar to Figure 1, substituting the terrestrial pole for position A and altering the great circle are AB to correspond to the observer's distance from the pole. When satisfied with the above figures, the Zenith Distance column should be covered and the remaining columns compared comparison of the Latitude and Altitude columns reveals an astronomical axiom that should be committed lastingly to memory; namely, that the "Altitude of the Pole equals the Latitude of the Observer". This axiom is rigorously true as a moment's consideration will make apparent. Every mile the observer moves away from the pole; that is, each latitude change of one minute occasions a change of one minute of angle, or arc, iii- the celestial pole's altitude and zenith distance, the former decreasing and the latter increasing when the observer moves away from the pole. If the observer moves toward the pole, the reverse is true. These facts can be readily seen if Figure 1 is carefully studied. In the southern hemisphere the rule still holds, the southern celestial pole, however, being considered instead of the north. The reader should satisfy himself on this point.

The axiom "The Altitude of Vas Pole equals the Observer's Latitude" was used unconsciously in sea navigation by many early peoples, - the Phoenicians, the Chinese, the Pacific Islanders and others, though the earth was assumed by them to be flat and latitude, as we consider it, unknown. However, the seafarers of these races were well aware of and acquainted with the change in the appearance of the heavens with change in latitude. They were adept at estimating the altitude of celestial bodies, by eye, to an astonishingly close figure. This ability and aforementioned knowledge were combined to great advantage by these early seamen. Steering well to the side of their destinations, these navigators would make good latitude, north or south, until the pole appeared at the proper altitude, that of the destination. A course toward the destination which would put, the pole abeam (an East or West course) would then be steered, since experience and word of mouth had taught these people that when plying such a course, the pole's altitude would not change. It was simple necessary to continue on such a course until the destination was reached.

The Hawaiian Islanders made many remarkable trips to Tahiti and return in open outrigger canoes (the distance between these ups is approximately 2,300 nautical miles) using their unconscious knowledge of the latitude axiom as their principle navigation aid. Figure 2 illustrates this.

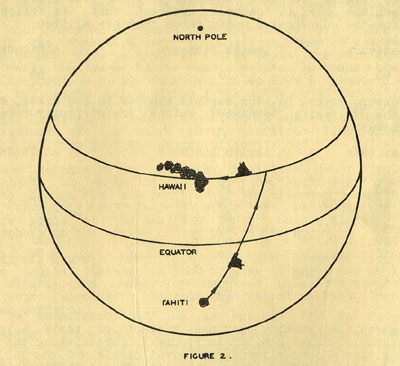
FIGURE 2.

It has been pointed out that a particular is small circle which connects all points on the earth from which heavenly body is found to have the same altitude, or the same zenith distance. In the special case in which the zenith distance is 90 and the altitude 0 degrees the position circle is a great instead of a small circle. The geographical position of a heavenly body was said to be the center of any position circle of that body; the zenith distance being its radius. From the tabulated values used to point out the latitude axiom, it will be seen that at a latitude of 30 degrees the pole's altitude is 30 degrees and its zenith distance 60 degrees. It is apparent that if the altitude of the celestial pole is 30 degrees when measured from one point on the 30th parallel of latitude it will be 30 degrees when measured from any point on that parallel. Since the 30th parallel connects all such points, it is clearly one of the position circles of the north celestial pole. If so, it must have the geographical position of the sky's pole, the terrestrial pole, as its center. This obviously is the case. If a position circle, the 30th parallel must have the zenith distance of the celestial pole as its radius. This, likewise, is apparent; the 30th parallel being everywhere 60 degrees distant from the pole. Since the 30th parallel conforms to all requirements; it must be a full-fledged position circle of the north celestial pole. Every other parallel of latitude in the northern hemisphere conforms to the same requirements and is a position circle of the north celestial pole; those of the southern hemisphere being position circles of the south celestial pole. The equator alone, of these position circles, is a great circle.

Figure 2 shows, in terms of position circles, the method of navigation employed not only by the Phoenicians, the Chinese, and Pacific Islanders, but by many sailing ships of comparatively modern times. The pole was approached or left until its altitude was found to equal the latitude of the destination. Thence an East or West course was sailed until the desired landfall was made. In the sailing ship era instruments were, employed for altitude measurements and the sun was usually used to determine, in a method later explained, the ship's latitude. However, the landfall was frequently made by sailing along that parallel of latitude passing through the destination.

In the practice of navigation, though little limitation exists in the matter of selecting bodies to observe, those at about 30 degrees altitude offer several advantages (to be pointed out later) and are generally selected for observation when possible. It has been pointed out that the 30th parallel of latitude is the position circle of a point in the sky (the celestial pole) whose altitude is 30 degrees. Keeping in mind the fact that position 'circles of this size are most frequently used a large scale conical map upon which this parallel appears should be consulted.

It should be noticed that the curvature of this parallel, and others near it, is very slight. Consequently, a moment's consideration makes apparent the fact that a straight line may be used to represent a portion of the position circle, a hundred mile length for example, with very little error resulting from the substitution. A straight line thus used to represent a small portion of a position circle is known as a "line of position" or "position line".

A position circle is generally a small circle. However, its radius is always a portion of a great circle; whose length equals the zenith distance of the particular heavenly body or point. The position circles of the celestial poles, the parallel of latitude as has been seen, have as their radii that portion of the terrestrial meridians included between the pole and the parallel. An inspection of any globe shows that all meridians and parallels intersect at right angles and it is quite evident from this that the radius of any position circle intersects that circle perpendicularly. Further, it is evident that the radius that contains the observer's position indicates the direction in which the observed body is seen from the observer's position. These are not special conditions applying only to the family of position circles now being considered. Imagine the meridians and parallels of either hemisphere, northern or southern, to appear on a tight-fitting transparent hemispherical cap. It is obvious that the characteristic's of the position circle family are not changed regardless of how the cap is slid over the surface of the globe.

If the altitude of any visible heavenly body is observed and the geographical position of that body located on the earth for the instant of observation, it should be apparent from the foregoing that a position circle can be drawn on the globe, and that the observer is somewhere on that circle. The zenith distance of the body, found from its altitude, is used as a radius and the circle is swung from the geographical position of the body as a center. Figure 3 shows a position circle drawn on the globe using the known geographical position of a heavenly body and a zenith distance found from a measured altitude.

FIGURE 3.

S is the body's geographical position and Z the position of the observer. Notice the angle A, at the observer's position included between the observer's meridian and the radius of the position circle. This is the azimuth of the observed body. The angle at the observer's position included by the observer's meridian and the radius of the position circle is, when measured clockwise, the bearing of the body measured from the north point on the observer's horizon. Thus the angle A conforms to the definition of azimuth.

It is often thought, and erroneously so, that an observer can obtain his position on the earth from an observation of one body, providing both the altitude and azimuth are measured. Theoretically this is possible.

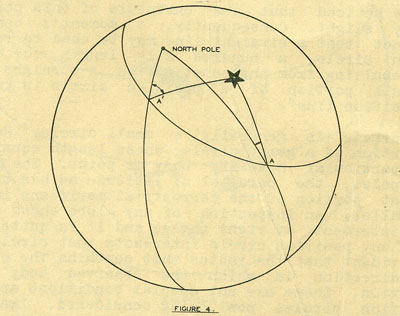
Figure 4 shows a position circle drawn from a measured altitude and known geographical position. The azimuth angles A and A', at two points on the circle, are indicated, and it should be carefully noted that these angles differ in magnitude. From this it maybe seen that the azimuth angle an observer measures changes as he travels around the position circle. Consequently, having measured the azimuth, a point on the position circle could be found at which the radius makes with the meridian at that point, angle equalling the measured azimuth. The intersection of the radius and position circle would then mark the observer's position. Theoretically this is quite correct. It is not practical, however, for the simple reason that the azimuth cannot be measured to the degree of accuracy required to permit such a procedure. Since it is quite difficult for beginning students of navigation to grasp this fact, an explanation of it will be valuable, and is warranted at this time.

Let the subject of terrestrial bearings in D. R. navigation be considered. From a theoretical position, A, on a chart or map, as in Figure 5 let the bearing of a prominent object B be determined. Suppose this bearing to be 60 degrees.

FIGURE 5

If a navigator actually measures the bearing of the point H as 60 degrees while flying, he is obviously on the line AB, (prolonged if necessary). This line is plotted on the chart from point B using the reciprocal of the bearing. Suppose the navigator in flight measures the bearing of point B as 60 degrees but that his measurement is one degree in error; the actual bearing of point B from his position being 59 degrees. The navigator plots line AB and believes himself situated on the line. However, due to the erroneous bearing measurement, he is actually on the dotted line. If the navigator's approximate distance from position B is 30 riles, then the resulting error is 1/2 mile. (1 degree equals 1 mile in 60).

Much the Same situation exists in the case of celestial bearings, or azimuths, except that the navigators position, instead of being only 30 miles distant from B (the geographical position) is several thousand miles removed. It is quite evident then that the error in position resulting from an azimuth one degree in error is of considerable magnitude. Since even a greater error must be expected in as azimuth measurement made in flight, an observation of a single body will only tell the navigator that, he is on a certain position circle. However, if the altitudes of two heavenly bodies are observed and their corresponding position circles are drawn, as in Figure 6, the navigator plainly must be at their intersection. The intersections of any two such circles are so far apart that the D. R. will tell the navigator at which intersection he is situated.

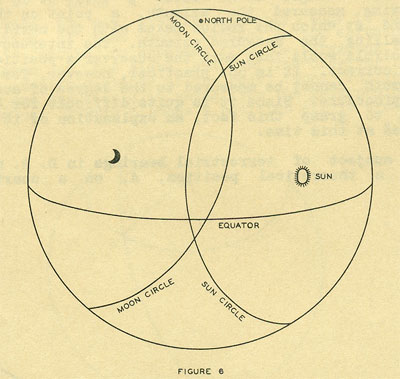
FIGURE 6

If a globe of suitable scale could be carried, the practice of celestial navigation would consist of measuring the altitudes of one or two bodies (two if available), of locating the geographical positions for the instant of observation, and of drawing the one or more position circles. Though only one position circle does not locate an observer on the earth, the information it furnishes is quite useful and valuable as will be seen in later chapters. Intersecting position circles, however, definitely locate the observer on the surface of the earth, since the D. R. can always be relied upon to tell the observer at which of the two intersections he is situated.

When working with maps and charts of the scale commonly employed in navigation practice, any such simple procedure as the above is out of the question. The navigator consequently is forced to use a much more devious process.

QUESTIONS AND ANSWERS

Q... Why is the term "bearing" used in the definition of azimuth?

A... A bearing may be measured with a surveyor's transit or a horizontal graduated circle upon which two vertical sights are mounted. It is readily realized that when using these iota the elevation of the reference point, or the point whose bearing is being taken is of no concern; the magnitude of the bearing angle being independent of such consideration and only dependent upon the angle through which the horizontal plate is rotated in sighting successively on the reference and the point whose bearing is wanted. Thus, a bearing clearly is an angle measured along the horizontal; along the observer's horizon, if the bubble or pendulum horizon is considered rather than the profile of the observer's landscape. The term bearing is used to impress the fact that azimuth is likewise independent of the elevation of either the reference or the point whose bearing is being taken; azimuth being the arc of the horizon intercepted between vertical circles passing through the two points (the reference and the body). The construction and use of a bearing plate, or surveyor's transit, implies "vertical circles" without mentioning them.

Q:.. Which of the celestial bodies cannot be assumed to be at an infinite distance from the earth?

A... The moon. The distance from the earth to the moon is but 239,000 statute miles. The neat nearest celestial body, the sun, is 93,000,000 statute miles distant from the earth. The star nearest the earth is 4 1/3 light years distant.

Q... Since the zenith distance of a body tells the observer's distance from the geographical position of that body, why is it not measured instead of the altitude?

A... No definite point marks the position of an observer's zenith. The accelerations of both surface and aircraft preclude positive indications of the horizontal or vertical by gravity operated mechanisms (liquids, bubbles, balls, pendulums, etc.). The visible horizon (see definition) is, on the other hand, quite positive and for this reason is always used when possible, from both air and surface craft. Therefore, the early instrument builders quite logically designed their instruments to measure altitude, since measurement was to be made from the visible horizon. For uniformity of practice, artificial horizon instruments were built to measure the same coordinate, though the gravity operated mechanisms of these instruments indicate the vertical (or the observer's zenith) as well as the horizontal.

Q... Though the star Polar is does not mark the exact position of the north celestial pole, can its altitude be used for latitude, as per the "latitude axiom"?

A... The altitude, of Polaris must be corrected before being taken as the latitude. The Nautical Almanac provides very simple and handy tables for this purpose, the use of which will be explained in a later chapter. The Rude Star Finder, also explained later, provides a quick means of correcting the altitude of Polaris to permit its use for latitude.

Q... Was the celestial pole depended upon entirely by the early races for position and direction?

A... No. The am and stars were used for direction and, in many areas; the constancy of the prevailing, seasonal winds for the same purpose. The pole, however, was depended upon for position; i.e., latitude.

In the atoll and island areas the natives were able to tell the direction of land by the visible effect such land had upon the shaping of the ocean swells. Many travelers of the South Seas have marvelled at the ability of the natives to unerringly point out the direction of land well beyond the range of vision after having been several days at sea; these natives having no knowledge of course or position.

Q... How is the geographical position of a heavenly body located?

A... The location of a geographical position of a heavenly body is a problem involving time and the Nautical Almanac. These will be studied in a later chapter.

Q... Is the azimuth of a celestial body ever used?

A... Yes. The equivalent of a measured azimuth is frequently used to check a craft's compass error. The accuracy needed in such work is not nearly that which would be necessary to locate the observer's point on his position circle and, consequently, its use for compass work is permissible and desirable. Also, the computed azimuth of a body is used to orientate the position lines of that body; the position lines running at right angles to the azimuth. The computed azimuth used for this purpose is exact (mathematically so) because it is calculated for an exact, known location, which has been arbitrarily chosen. Qbviously, since such an azimuth presupposes a known location, it cannot be used by the navigator to establish his location on his position circle. Such an azimuth would only locate the arbitrary point, if that point were on a known position circle.

Q.. How much error is occasioned in locating a point on a position circle if the measured azimuth to be used for this purpose is 1 degree in error?

A... While this is dependent upon several variables, an average figure is plus or minus 50 miles.